rightboys.blogg.se - Ar processes lasso procedure

AR PROCESSES LASSO PROCEDURE HOW TO
AR PROCESSES LASSO PROCEDURE SERIES

This is a very important concept in autoregression models and is also used in determining the order p of the autoregression model.

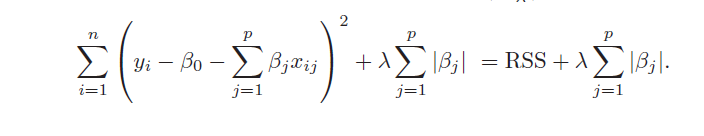
Remember, while learning about the AR (1) model, you had come across a term - autocorrelation.

AR PROCESSES LASSO PROCEDURE HOW TO

You must be wondering, how to determine the order p of the autoregression model? Later you will learn how to estimate these parameters using the ` statsmodel` library in Python. Determining these coefficients mathematically is little complex and is beyond the scope of this article. Some commonly used techniques are the Ordinary Least Square technique and the Yule-Walker equation. There are a number of ways available to compute the parameters 𝚽 p's. Here y t is assumed to have a correlation with its past p values and is predicted as a linear combination of past p values. This is the autoregression model of order p. , p) are the parameters of the model and c is the constant. Let’s see the form of the model when two lag values are used in the model. You can use more than one past term to predict the value at time t. In the above example, you saw how the value of y t is estimated using one past value (lag term), y t-1. Let us have a look at other orders of the autoregression model. You will be learning more about this later. Like the linear regression model, the autoregression model assumes that there is a linear relationship between y t and y t-1. The term autoregression means regression of a variable against its own past values. This is the autoregression model of order 1. Where 𝚽 1is the parameter of the model and c is the constant. You can estimate the relationship between the value at any point t, y t, and the value at any point (t-1), y t-1using the regression model as below. Let the observation at any point in time, t, be denoted as y t.

AR PROCESSES LASSO PROCEDURE SERIES

Instead of using a second time series (the stock price of BAC), the current value of the stock price of JPM will be estimated based on the past stock price of JPM. Now, let’s suppose you only have one series of data, say, the stock price of JPM. Where m is the slope of the equation and c is the constant.

Assuming that there is a linear relationship between X and y, the regression model estimating the relationship between x and Y is of the form.

Here, the stock price of JPM would become the dependent variable, y and the stock price of BAC would be the independent variable X.

Now you want to predict the stock price of JPM based on the stock price of BAC.

Thus, while working with a regression model, you deal with two variables.įor example, you have the stock prices of Bank of America (referred to as BAC) and the stock prices of J.P.

Python Implementation of Autoregression Modelsīefore you learn what is autoregression, let’s recall what is a regression model.Ī regression model is a statistical technique to estimate the relationship between a dependent variable (y) and an independent variable (X).

Visualising ACF Plot and PACF Plot in Python.

Autocorrelation Function (ACF) Plot & Partial Autocorrelation Function (PACF) Plot.

Autocorrelation & Partial Autocorrelation.

Autoregression Models of Order 2 and generalise to order p.

In this article you will learn about one such model, the Autoregression Model or the AR Model. There are a number of time series models available to make these predictions. The time series models analyses and trains the model on the past data to make future predictions. observed in the past data, a time series model predicts the value in the next time period. These time intervals can be regular or irregular. Time-based data is data observed at different timestamps (time intervals) and is called a time series. Time series modelling is a very powerful tool to forecast future values of time-based data.